BOPE-GPT

bope-gpt

Brought to you by Ricardo Valencia Albornoz, Yuxin Shen, Sabah Gaznaghi, Clara Tamura, Ratish Panda, Zartashia Afzal and Raul Astudillo

Youtube video: Video

Reduced slide set for video: Slides

Full slides by Zartashia Afzal: Slides

App prototype developed by Ratish Panda: App

All authors contributed significantly to the project. A CRediT authorship statement is available at the end of the README

The first steps

Analysing the Fischer-Tropsch dataset from the point of view of classical single and multi-objective BO

Fischer-Tropsch Synthesis represents a pivotal process in the field of industrial chemistry, serving as a cornerstone for the production of liquid hydrocarbons from carbon monoxide and hydrogen gases. Developed by German chemists Franz Fischer and Hans Tropsch in the early 1920s, this method provides a versatile pathway for converting syngas—a mixture of hydrogen and carbon monoxide derived from coal, biomass, or natural gas—into a variety of valuable hydrocarbon products, including fuels and alkanes. The process is particularly adopted for its ability to produce clean, sulfur-free fuels, which are crucial in today’s efforts towards environmental sustainability and energy security. Through catalytic chemical reactions conducted at high temperatures and pressures, Fischer-Tropsch Synthesis offers a strategic approach to mitigating reliance on crude oil by leveraging alternative carbon sources, thereby playing a critical role in the evolving landscape of global energy.

The Fischer-Tropsch synthesis is a chemical reaction that converts a mixture of carbon monoxide (CO) and hydrogen gas (H₂) into liquid hydrocarbons.

\[n CO + (2n+1) H_2 \rightarrow C_nH_{2n+2} + n H_2O\]

The ground truth we use here is the Artificial Neural Network model built from the dataset in the paper (Chakkingal, Anoop, et al., 2022), with four inputs: space-time (W/F_CO), syngas ratio, temperature and pressure, and four outputs: y1 as the carbon monoxide conversion, y2 as the selectivity towards methane (SCH₄), y3 as the selectivity towards paraffins (SC₂−C₄) and y4 as the selectivity towards light olefins (SC₂−C₄=).

Maximizing all of the four outputs is desirable for this process. However, in reality some of the three products are considered as byproducts, and the ones you care only achieve high selectivity under very intensive conditions, which are not feasible in technical terms or economical terms. Therefore, we can adjust the objective settings in th BO routine and make the optimization problem more adapted to what would be a real situation.

When you have a ground truth available, classical single objective and multi-objective BO are your start points. These provide useful insight in the nature of each output,i.e, its range, monotonocity, correlations, etc., that are important when working afterwards with preferential Bayesian Optimization.

Single-objective BO implementation

We conducted single-objective BO implementation for four different outputs respectively. The model we use is the SingleTaskGP, and qExpectedImprovement is used as the acquisition function.

The single-objective BO works quite well, and all four outputs are close to 1 (the upper bound after normalization) following optimization. A problem arises because the optimal input conditions differ for each of the four outputs. Therefore, it is not possible to achieve the optimum for all four outputs simultaneously.

Multi-objective BO implementation

We saw that the single-objective BO work quite well when optimizing the four different outputs separately, but the four outputs includes potential trade-offs, and the optimal value cannot be reached at the same time. We then implemented multi-objective BO to explore the pareto front in the Fischer-Tropsch dataset and identify poteintial trade-offs. We keep the SingleTaskGP as the model, and the qExpectedHypervolumeImprovement as the acquisition function to see the pareto front. By looking at the pairwise comparision of the output pairs, we found for some pairs of the output, the trade-off is quite clear (e.g. output 1 and output 3). However, some of them are hard to identify (e.g. output 3 and output 4).

Into the preference world

From the multi-objective BO, we observed that the multi-objective optimization result could be a very hard task. Since it is often hard in situ to have the exact utility function over those objectives, it is much easier for people to make pairwise comparisons. Therefore, we introduced a preference setting to the Fischer-Tropsch problem, and expect the LLM to do the pairwise comparison.

Decision by a comparison function

We first used a comparison function to conduct the decision step and test the preference setting. The model we use here is PairwiseGP, and the acquisition function AnalyticExpectedUtilityOfBestOption (EUBO) can help us to find the best observed value under the preference setting.

Decision by an LLM & Comparison of different objective functions

Finally we turned to the pairwise comparison by LLM. Basically, we modify the pairwise comparison generation function in the Botorch tutorial section here, so that the comparison by utility function can be replaced by the decision of an LLM. The large language model we used was provided by Cohere; we are using the Cohere LLM API trial keys that allows us to perform free chat queries to the model with a restriction of 20 API calls/minute and 1000 API/month.

We explored different cases below: (“” means prompt to the LLM, [] indicates objective utility function we tell the EUBO. And we compare the performance of the two results for the optimal values to see if LLM can replace numerical decision)

1. “The four outputs are equally important, and we want to maximize all of them.” [obj: maximize sum of y1-y4] notebook

The optimized sum can reach ~3.1, which is reasonable for the dataset and the model.

1. “We only want to maximize the CO conversion.” [obj: maximize y1] notebook

The optimized sum can reach ~1, which is the maximal value after MinMax normalization.

1. “The light olefins (y4) is considered as a negative output and we want to minimize y4 while maximizing the other three objectives (y1-y3).” [obj: maximize y1+y2+y3-y4] notebook

*4. A dual case of the first objective (with typo in prompt)

“The four outputs are equally important, and we want to ‘minimize’ all of them.” [obj: maximize sum of y1-y4] notebook

In this case, we modified the prompt with a typo, and keep all the other utility & target function as the same with case 1. From the results, we can see that the performance of EUBO-LLM with typo is lower than random. The LLM with typo changes the whole meaning of the prompt, showing the importance of the prompt.

From the result of the above three cases, we can see that the LLM (EUBO-LLM in the plot) is working very well for the first two cases (similar performance to EUBO/synthetic utility function) and can identify the requirement of the process by changing the prompts. In the third case, the performance is close to Random Exploration, and we hypothetise that the LLM cannot interpret this scenario or understand the utility function from the prompt alone.

To understand how the process work behind the scenes, we can have a look to a sample prompt:

Suppose you're managing a Fischer-Tropsch synthesis process, Option A: regime of 0.6 CO conversion, 0.0 methane production, 0.1 paraffins, 0.8 light oleffins. Option B: regime of 0.8 CO conversion, 0.1 methane production, 0.2 paraffins, 0.6 light oleffins. Choose only one option, only answer with 'Option A' or 'Option B'

The numbers from the model output are entered to prompt as strings with one decimal, to simplify the input and provide some fuzziness in the LLM decision (after prompt engineering, we realise that numbers with many decimals are not well intepreted by the Cohere LLM). Now, testing some of the cases before means translating (perhaps subjetively) the utility function into a prompt context that the LLM can take. For case 1 e.g. the equally important outputs means that the utility function is a (equally weighted) linear combination of the outputs, but when applying this in the LLM context for comparison, we need to change the context prompt to something like this:

Suppose you're managing a Fischer-Tropsch synthesis process, and you consider that every output of the process is equally important, you have two options, Option A: regime of 0.6 CO conversion, 0.0 methane production, 0.1 paraffins, 0.8 light oleffins. Option B: regime of 0.8 CO conversion, 0.1 methane production, 0.2 paraffins, 0.6 light oleffins. Choose only one option, only answer with 'Option A' or 'Option B'

An app to rule them all

An app to perform preferential BO optimisation using the LLM pairwise comparison function, shown in the previous plot as EUBO-LLM, was developed by Ratish Panda, and it’s available at https://bope-gpt.vercel.app/

Frontend

The Next.js framework was used for the frontend of this app, with an instance deployed on Vercel. View the source code at frontend/.

To run locally, clone the frontend/ code and make sure you have Node.js installed for a Typescript runtime to build the frontend locally. Then install the dependencies listed in package.json with npm install and run with npm run dev or npm run build to build and deploy the frontend to a local port.

Backend

The current backend computing and serving requests made from the BOPE-GPT app frontend is a FastAPI app deployed on a personal local VPS at bopegpt.ratishpanda.me. Requests are routed through an Nginx proxy via a local Unix socket and passed to a running Gunicorn server with 2 Uvicorn workers. This isn’t a powerful VPS, so compute and processing may be slow! As an alterative, for faster processing on more powerful local machines, you can clone this repo locally and build the frontend and backend locally and run it on your data that way. You will have to procure a personal MongoDB Atlas URI key and Cohere API Key for local use however.

For more info on the structure of the backend app and running locally, navigate to backend/fastapi_backend/readme.md in this repository where this is detailed further!

Screenshots

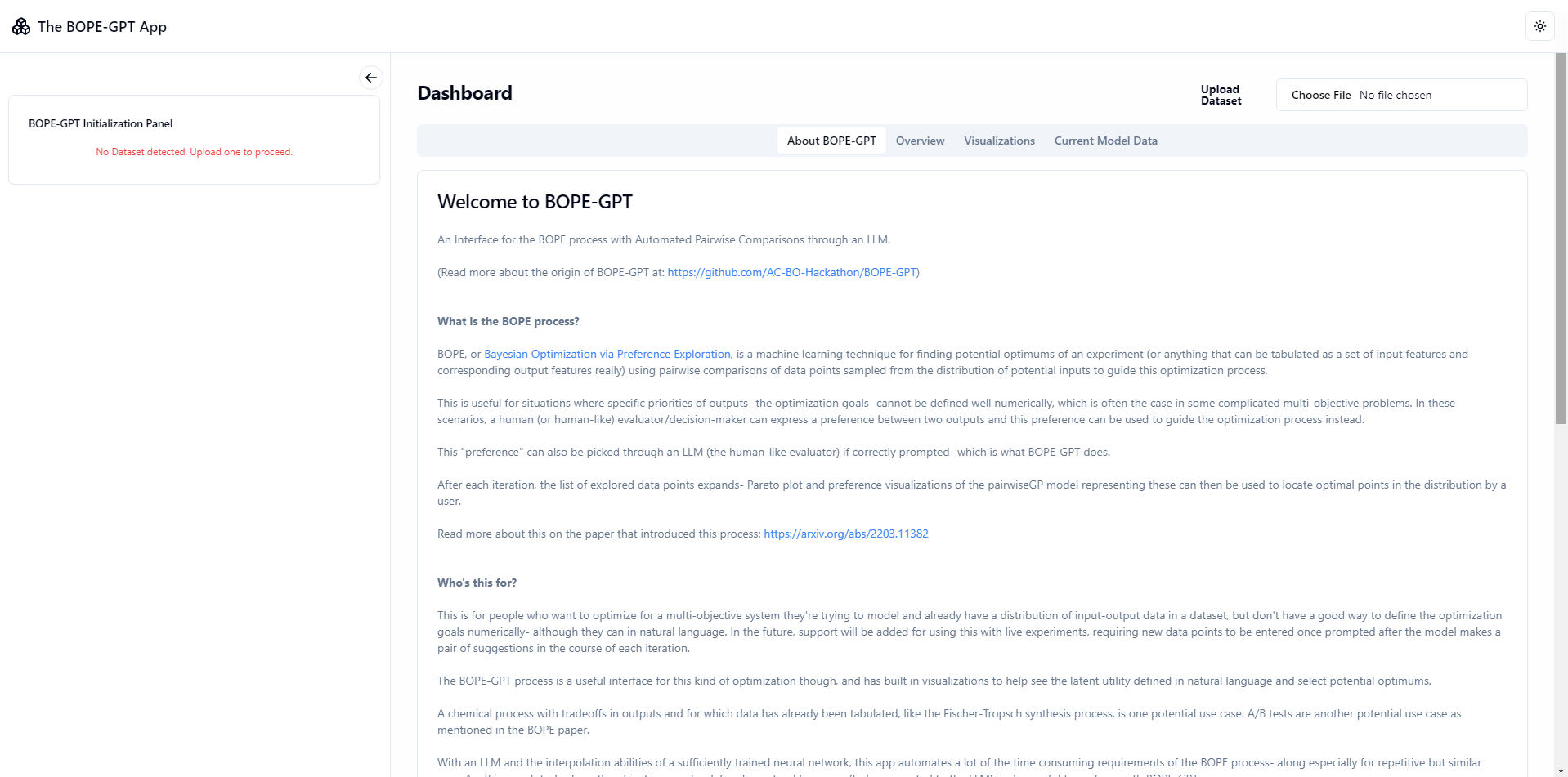
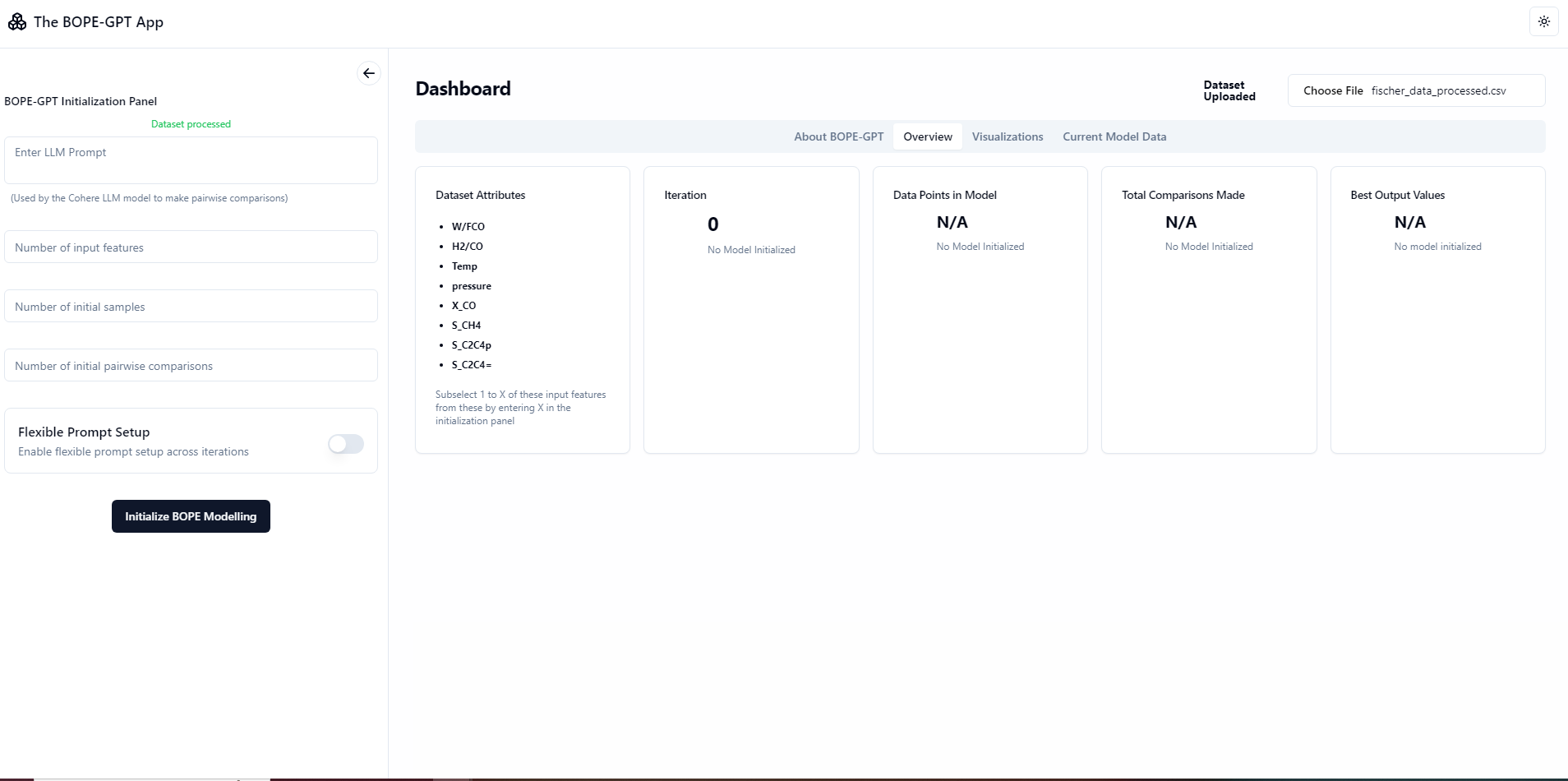
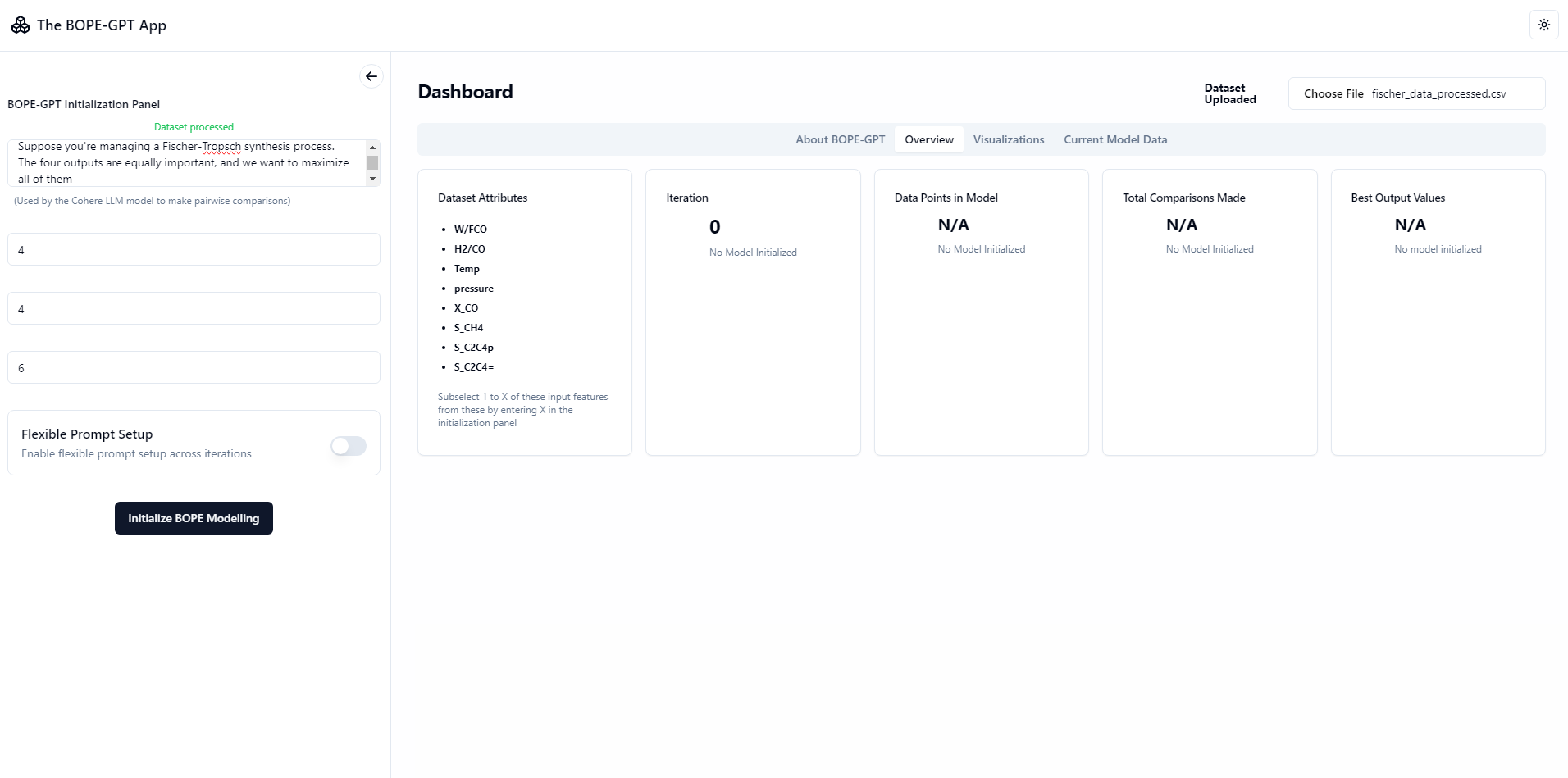
NOTE: Loading can take upto a few minutes, lots of compute required + the VPS used for the free live backend is a personal one and not so powerful! Keep the tab open while waiting for a response. Run locally for faster loading times if you have a powerful system.

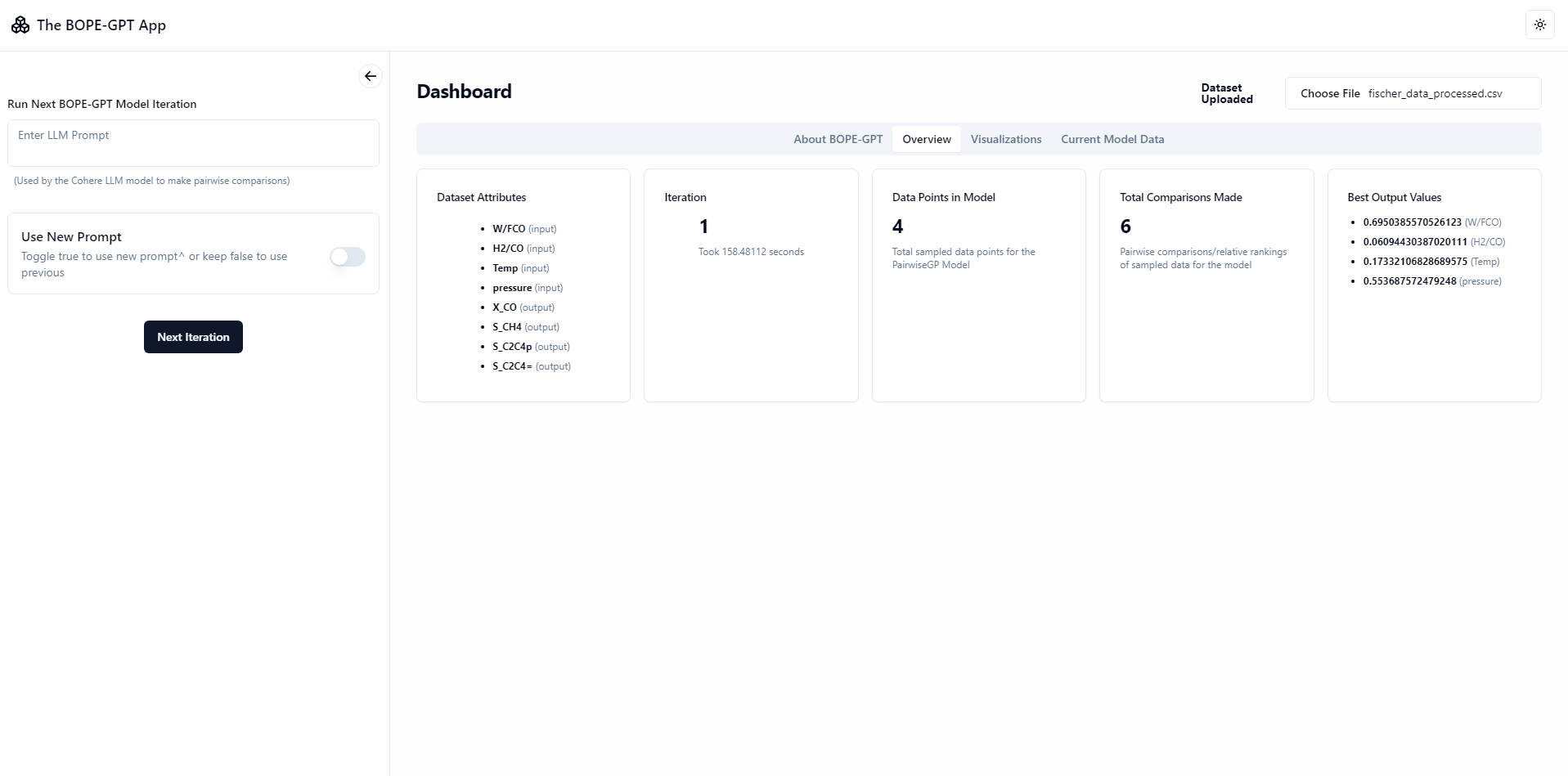
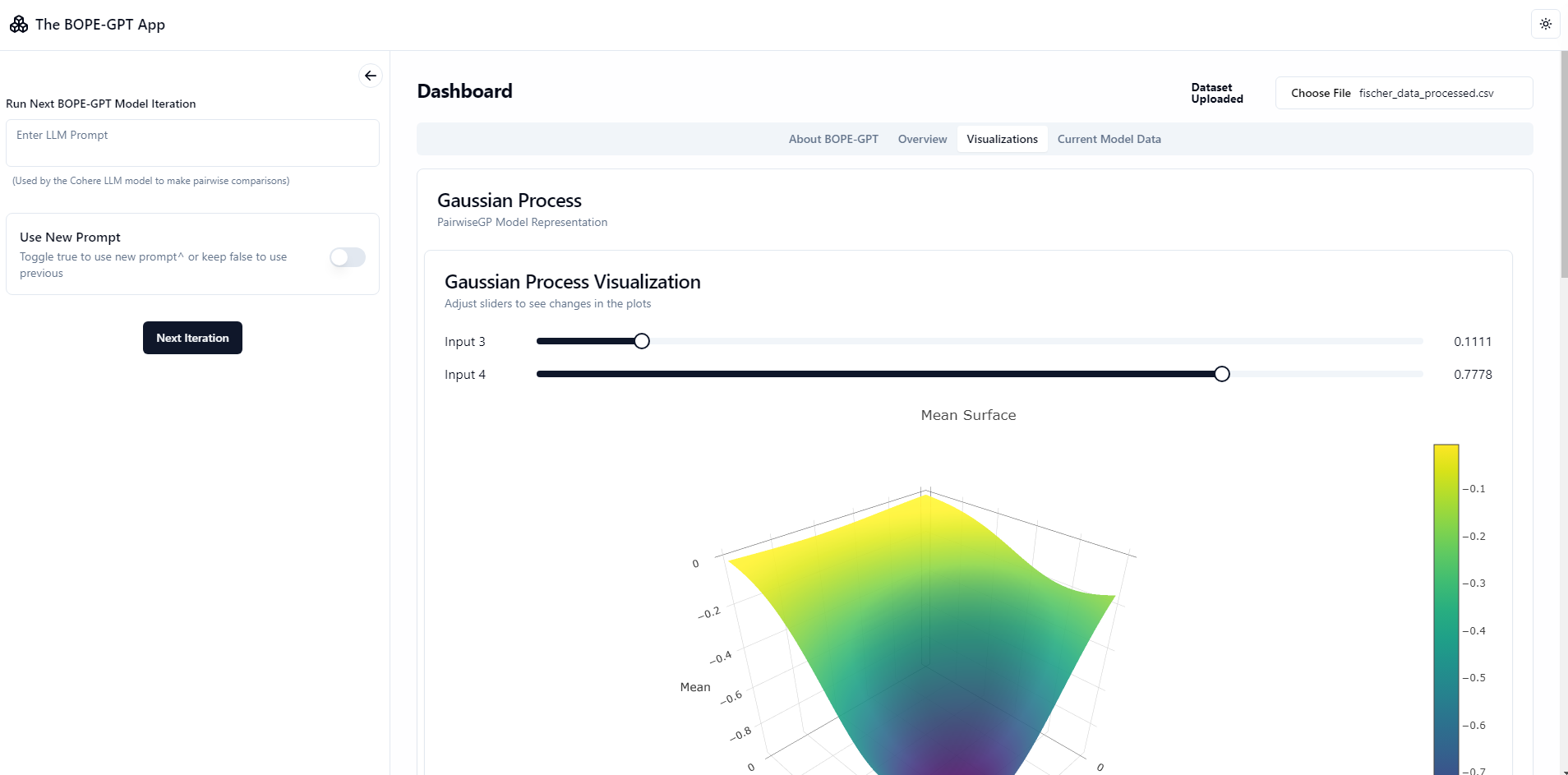
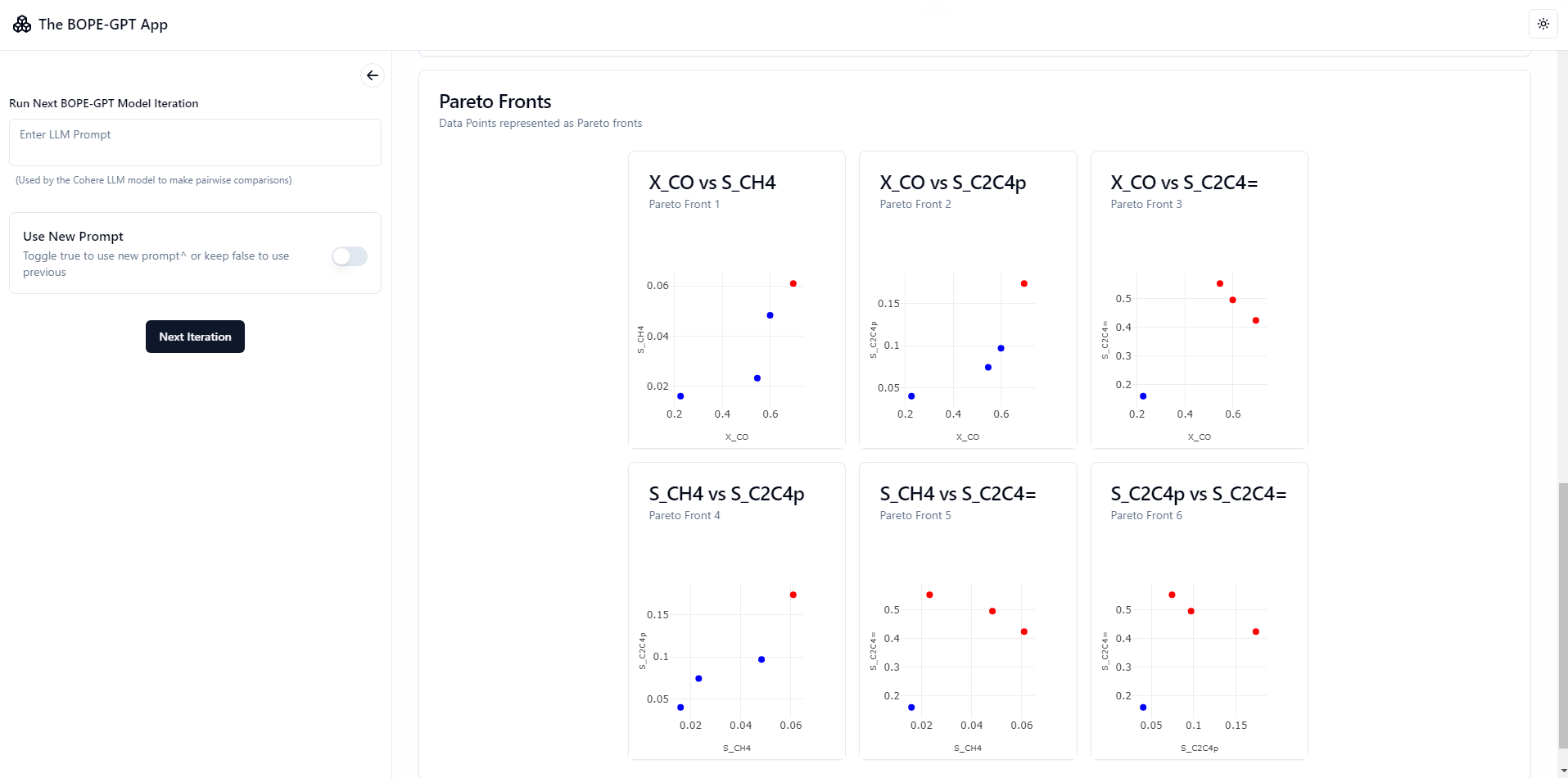
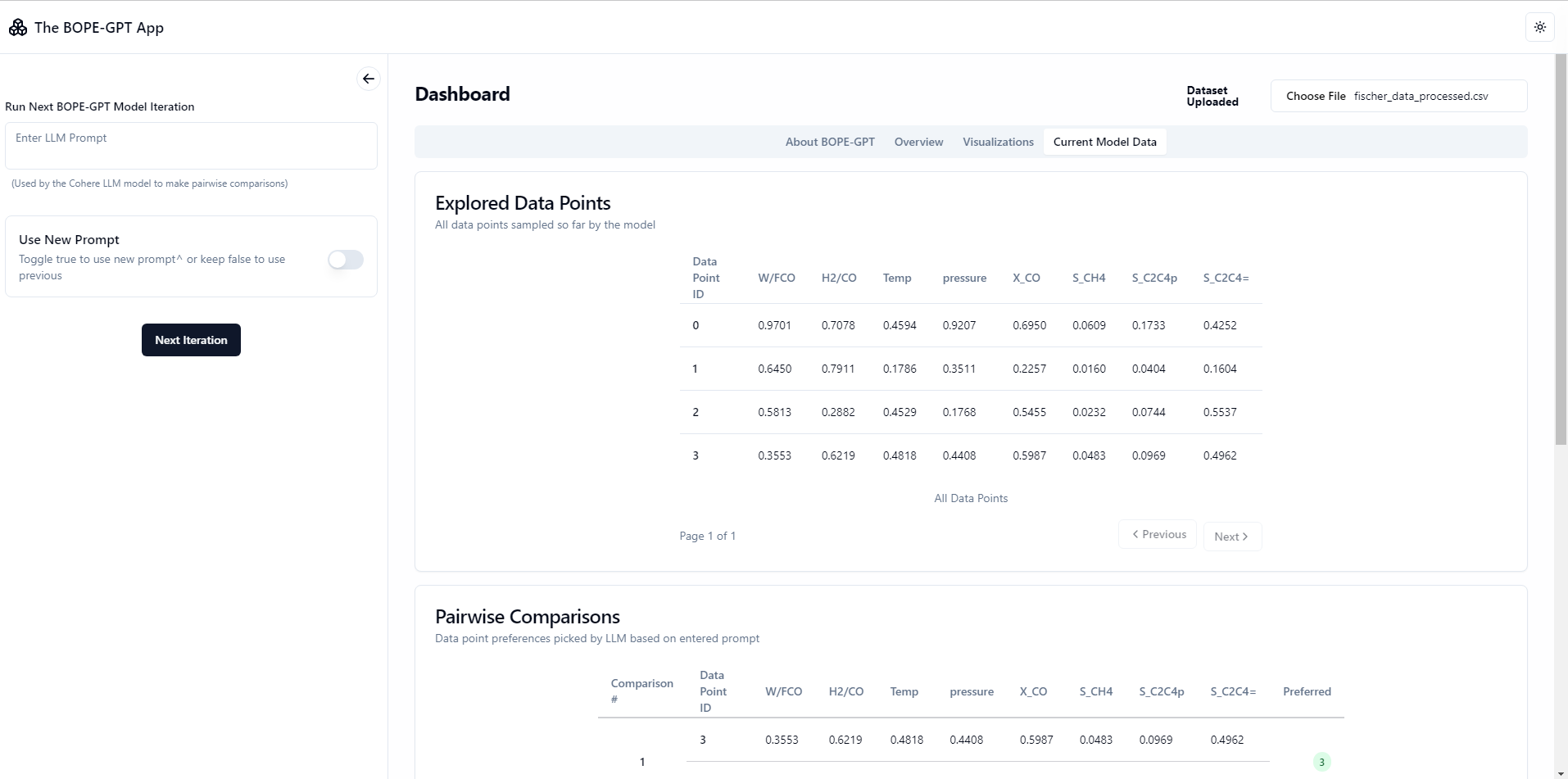
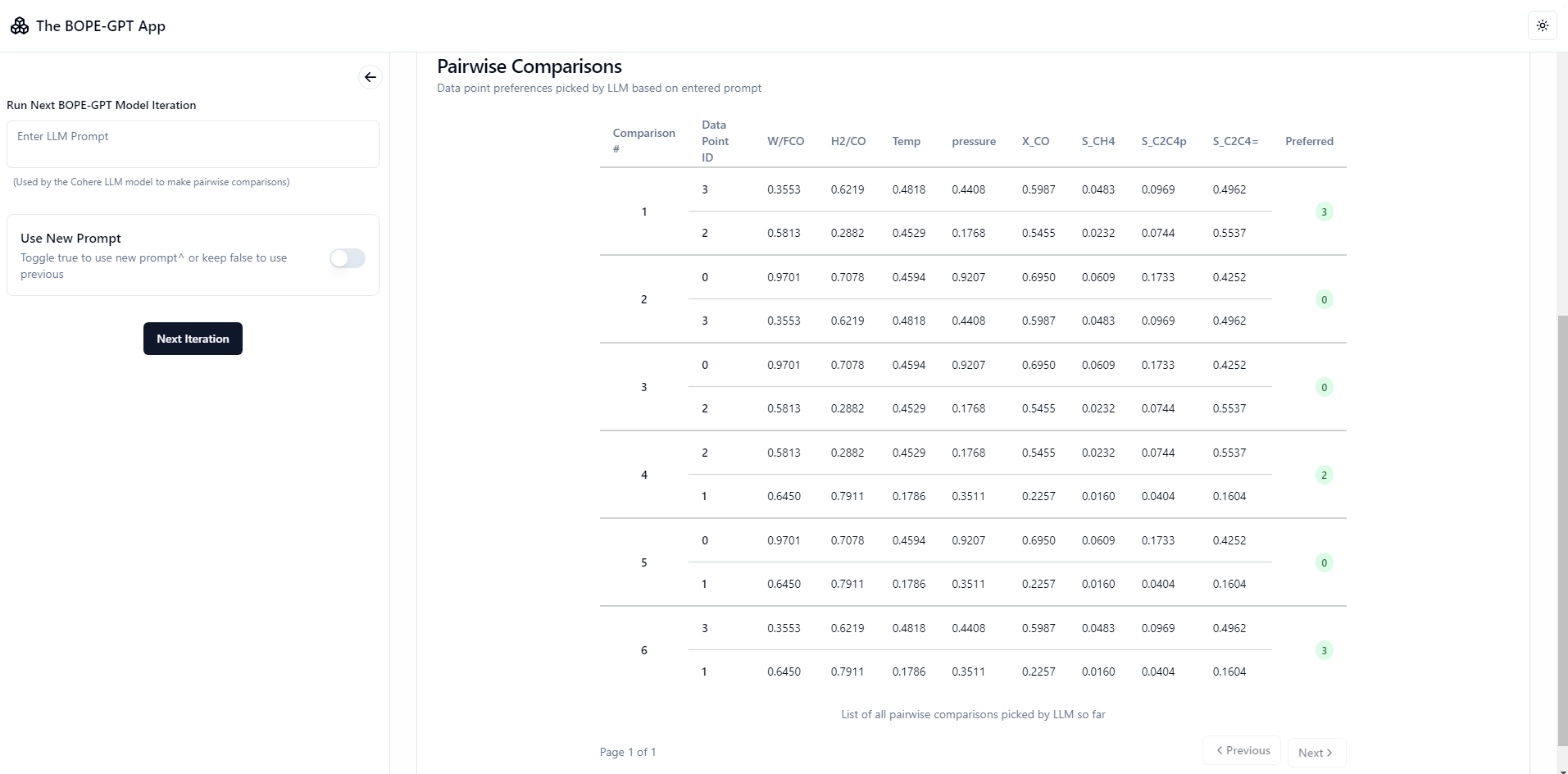
Interactive GP Visualization and Pareto Plots

Miscellaneous

Environment To run the code, we’re typically updating a conda/mamba environment that, on the first time, can be installed using the following commands:

mamba create -n botorch_mar2024 pytorch torchvision torchaudio pytorch-cuda=11.8 python==3.11 -c pytorch -c nvidia

mamba install botorch matplotlib seaborn -c pytorch -c gpytorch -c conda-forge

mamba update -c conda-forge ffmpeg

mamba install -c conda-forge dash

pip install keras

pip install tensorflow

pip install cohere

Seeding Remember to define the seed for random generators when comparing different algorithms:

#Your chosen seed your_seed = 42

random.seed(your_seed)

np.random.seed(your_seed)

torch.manual_seed(your_seed)

torch.backends.cudnn.deterministic = True torch.backends.cudnn.benchmark = False

torch.cuda.manual_seed(your_seed) torch.cuda.manual_seed_all(your_seed)

References

1. BoTorch tutorial for Preference BO.
2. BoTorch tutorial for BOPE.
3. González J, Dai Z, Damianou A, Lawrence ND. Preferential Bayesian Optimization. In: Proceedings of the 34th International Conference on Machine Learning. PMLR. pp. 1282–1291.
4. Lin ZJ, Astudillo R, Frazier P, Bakshy E. Preference Exploration for Efficient Bayesian Optimization with Multiple Outcomes. In: Proceedings of The 25th International Conference on Artificial Intelligence and Statistics. PMLR. pp. 4235–4258.
5. Lozano-Blanco G, Thybaut JW, Surla K, Galtier P, Marin GB. Single-Event Microkinetic Model for Fischer−Tropsch Synthesis on Iron-Based Catalysts. Ind Eng Chem Res 2008;47:5879–5891.
6. Chakkingal A, Janssens P, Poissonnier J, Virginie M, Khodakov AY, et al. Multi-output machine learning models for kinetic data evaluation : A Fischer–Tropsch synthesis case study. Chemical Engineering Journal 2022;446:137186.
7. Qin Z, Jagerman R, Hui K, Zhuang H, Wu J, et al. Large Language Models are Effective Text Rankers with Pairwise Ranking Prompting. DOI: 10.48550/arXiv.2306.17563.
8. Balandat M, Karrer B, Jiang DR, Daulton S, Letham B, et al. BoTorch: A Framework for Efficient Monte-Carlo Bayesian Optimization. Epub ahead of print 8 December 2020. DOI: 10.48550/arXiv.1910.06403.

CRediT statement

Ricardo Valencia Albornoz: Conceptualization, Methodology, Software (notebook), Validation, Formal analysis, Writing - README, Visualization, Project administration

Yuxin Shen: Conceptualization, Methodology, Software (notebook), Validation, Formal analysis, Data Curation, Writing - README, Visualization, Project administration

Sabah Gaznaghi: Methodology, Software (notebook), Validation, Formal analysis, Writing - README, Visualization

Clara Tamura: Methodology, Software (notebook), Validation, Formal analysis, Writing - README, Visualization

Ratish Panda: Software (app), Validation, Formal analysis, Writing - README, Visualization, Investigation, Resources

Zartashia Afzal: Software (presentation), Validation, Formal analysis, Writing - README, Visualization, Investigation, Resources

Raul Astudillo: Methodology, Software (notebook), Validation, Formal analysis, Writing - Review & Editing, Supervision

This site is open source. Improve this page.